7013. Дороги Абсурдистана

Народ Абсурдистана обнаружил как строить дороги только в прошлом году. После открытия каждый город решил построить свою дорогу, соединяющую свой город с некоторым другим городом. Каждая новая дорога может использоваться в обоих направлениях.

Абсурдистан полон удивительных совпадений. Для строительства дорог всем n городам потребовался всего один год. И что еще более удивительно, в конце концов можно было путешествовать из каждого города в любой другой город, используя недавно построенные дороги.

Вы купили справочник туриста, в котором нет карты страны с новыми дорогами. Он содержит только огромную таблицу с кратчайшими расстояниями между всеми парами городов, использующими недавно построенные дороги. Вы хотели бы знать, между какими парами городов существуют дороги и какова их длина, потому что Вы хотите восстановить карту n недавно построенных дорог из таблицы кратчайших расстояний.

Вход. Для каждого теста:

· Строка содержит число n (2 ≤ n ≤ 2000) – количество городов и дорог.

· n строк по n чисел. j-ое число i-ой строки содержит кратчайшее расстояние между городами i и j. Все расстояния между двумя различными городами положительны и не более 10⁶. Расстояние от i до i всегда равно 0, а расстояние от i до j равно расстоянию от j до i.

Выход. Для каждого теста вывести n строк с тремя целыми числами a b c описывающих дорогу между городами a и b (1 ≤ a, b ≤ n) длины c (1 ≤ c ≤ 10⁶), где a ≠ b. Если существует несколько решений, то вывести любое, дороги можно выводить в любом порядке. Гарантируется, что хотя бы одно решение всегда существует.

Между каждой парой тестов следует выводить пустую строку.

Пример входа	Пример выхода
4 0 1 2 1 1 0 2 1 2 2 0 1 1 1 1 0 4 0 1 1 1 1 0 2 2 1 2 0 2 1 2 2 0 3 0 4 1 4 0 3 1 3 0	2 1 1 4 1 1 4 2 1 4 3 1 2 1 1 3 1 1 4 1 1 2 1 1 3 1 1 2 1 4 3 2 3

РЕШЕНИЕ

система непересекающихся множеств

Анализ алгоритма

В связном графе из n вершин заданы кратчайшие расстояния между всеми парами вершин. Необходимо восстановить ребра графа.

Построим минимальное остовное дерево графа. Его n – 1 ребро являются ребрами искомого графа. Остается найти еще одно ребро. Найдем ребро наименьшего веса, не входящее в минимальный остов – оно и будет последним искомым ребром.

Пример

Для первого теста матрица кратчайших расстояний и один из соответствующих ей графов имеют вид:

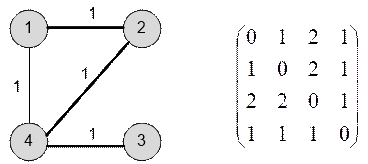
Ребра, входящие в минимальный остов, выделены жирными линиями.

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 2010

int mas[MAX], depth[MAX], d[MAX][MAX];

Объявим класс ребро. Ребро соединяет вершины u и v, имеет длину w. Сортировать ребра будем по их длине – для этого объявим встроенный компаратор.

class edge

{

public:

int u, v, w;

edge() : u(0), v(0), w(0) {}

edge(int u, int v, int w) : u(u), v(v), w(w) {}

int operator< (const edge &e) const

{

return w < e.w;

}

};

Список ребер графа храним в векторе e.

vector<edge> e;

Функция Repr возвращает представителя множества, в которое входит вершина n.

int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

Функция Union объединяет множества, которым принадлежат вершины u и v. Используем эвристику по глубине. В матрицу d заносим веса построенных ребер: если u и v принадлежат разным множествам, то ребро между ними принадлежит остову и является ребром искомого графа, в таком случае заносим d[u][v] = w.

int Union(int u, int v, int w)

{

int u1 = Repr(u), v1 = Repr(v);

if (u1 == v1) return 0;

if (depth[u1] < depth[v1]) swap(u1,v1);

mas[v1] = u1;

if (depth[u1] == depth[v1]) depth[u1]++;

d[u][v] = d[v][u] = w;

return 1;

}

Функция ReadGraph читает входной граф. Ребра запоминаем в векторе e.

void ReadGraph(void)

{

int i, j, dist;

for(i = 1; i <= n; i++)

for(j = 1; j <= n; j++)

{

scanf("%d",&dist);

if (i < j) e.push_back(edge(i,j,dist));

}

}

Основная часть программы. Читаем ребра графа и сортируем их по возрастанию длин.

while(scanf("%d",&n) == 1)

{

e.clear();

ReadGraph();

sort(e.begin(), e.end());

Инициализируем n множеств. Инициализируем массивы. Изначально ни одно ребро не принадлежит минимальному остовному дереву, поэтому положим d[u][v] = ∞.

for(i = 1; i <= n; i++) mas[i] = i;

memset(depth,0,sizeof(depth));

memset(d,0x3F,sizeof(d));

Строим минимальный остов, выводим на лету его n – 1 ребро.

for(i = 0; i < e.size(); i++)

if (Union(e[i].u,e[i].v,e[i].w))

printf("%d %d %d\n",e[i].u,e[i].v,e[i].w);

Ищем последнюю дорогу – ребро минимальной стоимости, которое не входит в остов. Ребро (u, v) не входит в остов, если d[u][v] = ∞.

for(i = 0; i < e.size(); i++)

if (d[e[i].u][e[i].v] == 0x3F3F3F3F)

{

printf("%d %d %d\n",e[i].u,e[i].v,e[i].w);

break;

}

Между каждой парой тестов выводим пустую строку.

printf("\n");

}